‘π’ is a number that you may already be familiar with. It is approximately equal to 3.14 although nobody knows its exact value.
The number is well known for featuring in the formulae;
Area = πr
Circumference = π D
2
Wherever circles and spheres are found, π will not be far away.
William Jones (1675 - 1749) introduced the symbol 'π' in 1706. It was later popularised by the great mathematician Leonhard Euler (1707-1783).
[The Secret] Life of π
A look beneath the surface of a familiar number
‘π’ is a number that you may already be familiar with. It is approximately equal to 3.14 although nobody knows its exact value.
The number is well known for featuring in the formulae;
Area = πr
Circumference = π D
2

Wherever circles and spheres are found, π will not be far away.
These formulae tell us how to find the area and circumference of any circle if we know the radius or diameter.

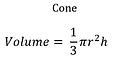
π also appears in the formulae for the area and volume of ellipses, cones, cylinders, ellipsoids and spheres. Wherever circles and spheres are seen, π will not be far away.
You can find π on your calculator. If you convert π to a decimal, then you will see something like 3.14159265 on your screen.
However, that is only the beginning of the story of one of the most famous and intriguing numbers in the whole of mathematics.
π appears again and again in a huge number of seemingly unrelated areas. It appears in many other subjects than mathematics.
π is fascinating in its own right. It has a rich history, stretching back to the earliest human societies.
Records exist from over 2,000 years ago showing that the value of π had already been calculated to two decimal places in Ancient Greece.
By 500 AD, Chinese mathematicians had achieved seven digits of accuracy. This was an incredibly impressive feat for the time and it was not improved upon for more than a thousand years.
By the nineteenth century, π had been calculated to 126 decimal places. Later, once computers became common, the number of known digits increased rapidly. Today trillions of digits are known.
William Shanks (1812-1882) worked for many years to find the first 707 digits of π. Unfortunately, he made an error at the 527th decimal place and all of the following digits were wrong!
In November 2016, π was calculated to over 22.4 trillion decimal places by π fan Peter Trueb who built his own computer with seven hard drives to tackle the task (most computers have one).
In March 2019, Emma Haruka Iwao of Japan smashed the record, increasing it to 31 trillion digits. She has indicated that she is keen to find more digits in the future.
It would seem that there is no end to π but there will always be many people keen to push our knowledge of the famous number even further.
π is an irrational number which means it can never be written as a fraction, although we can get very close to the true value of 3.141592653589793238462643383279502884197169399375105820974944592.....


The decimal expansion of π goes on forever and there is no regular pattern within the digits. A consequence of this is that you should be able to find your birthday (e.g. 19/01) in the digits of π!
If you are very determined then you can find your full birthday (i.e.19/01/06), your telephone number or any run of digits that you choose.
In fact, if we let a = 1 , b = 2 , c = 3,... etc. (letting the two digit sequence 10 stand for 'k', 11 for 'l' etc.), then you will eventually be able to find the whole of your name within the digits of π. For example, “David” (this name would be coded as 412294) first appears at decimal place 206,399.
Somewhere in the digits of π may lurk the complete works of William Shakespeare!
In the novel ‘Contact’ by Carl Sagan, the main character finds a message deep in the digits of π which reveals profound hidden secrets about the universe which humans had been unaware of.
Despite the apparent randomness in the digits of π, it does appear to be normal. This means that whilst the digits appear as if at random, in the long run there seems to be approximately the same proportion of each digit.
π is also a transcendental number which means that it can never be the solution of any equation with rational coefficients such as:

You will continue to meet π throughout your mathematical studies. The number is found in all sciences, engineering and of course mathematics. There are even artists who use π as their inspiration.
William Jones (1675 - 1749) introduced the symbol 'π' in 1706. It was later popularised by the great mathematician Leonhard Euler (1707-1783).
There are no occurrences of the sequence '123456' in the first million digits of π but the sequence '12345' appears eight times.